|
Achtergrondinformatie zie: "Zeven Invalshoeken voor Vakdidactiek"
Samenvatting
In de blog over Het verborgen pad is uiteengezet hoe de berekening van een onekende grootheid op basis van een aantal gegevens vorm gegeven kan worden met een PAD (probleem Analyse Diagram). Diezelfde techniek is te gebruiken voor het uitvoeren van berekeningen die verpleegkundige moeten maken om de jusite docering van medicijnen te berekenen.
Naast het overzicht van handelingsvoorschriften is ook het rekenen met eenheden van het grootste belang voor verpleegkundigen. Elke stap in de berekening is niet alleen een bewerking van getallen, maar ook een bewerking van eenheden. In de blog Het gebruik van eenheden is al aangegeven hoe eenheden zich laten bewerken als breuken..
Voorbeeld 3.3 bij blog nummer 3
Expliciteren van het instructieproces tijdens het onderwijs"
Verpleegkundig rekenen bijvoorbeeld
Wat is verpleegkundig rekenen?
Verpleegkunidg rekenen is het uitvoeren van brekeningen die samenhangen met de toedining van injecties, het oplossen van medicijnen, het klaarzetten van infusen, het verzorgen van het zuurstofverbruik en al dat soort ondersteunende medische hulpmiddelen.
Aangezien de gezondheid en zelfs het leven van mensen af kan hangen van de juiste berekeningen, is het een belangrijk onderdeel in de opleiding van verpleegkundigen. HBO-studenten moeten een reeks vraagstukken foutloos kunnen oplossen en MBO-studenten mogen maximaal 1 fout maken, omdat zij onder supervisie van een HBO-verpleegkundige staan.
Er zijn diverse boeken die het verpleegkundig rekenen uitvoerig behandelen. Als bijlesdocent heb ik ter ondersteuning van die berekeningen een aparte website over Verpleegkundig rekenen aangemaakt. Als illustratie voor deze blogs over vakdidactiek haal ik een dtype vraagstuk eruit om te demonstreren dat het verborgen pad en de bewerking van eenheden ook op dit vakgebied zeer goed bruikbaar zijn.
Voorbeeldopgave: een injectie gereed maken
De opgaven bij verpleegkundig rekenen komen sterk overeen met de opgaven bij bedrijfseconomie: er is een aantal gegevens en een onbekende grootheid waarvan de waarde berekend moet worden.
Mevrouw de Vries (81 kg) moet per dag 1 IE insuline per kg lichaamsgewicht krijgen, verdeeld over 3 injecties. In voorraad is een insuline-oplossing van 100 IE / ml.
Hoeveel ml moet zij hiervan krijgen per injectie?
1. Oriëntatie op de opgave
De vraag uit de opgave gaat over ml per injectie (ml / injectie). Daarvoor zijn als eenheden gegeven: kg, IE, IE / kg, aantal injecties en IE / ml. Deze vraag richt zich op een getal, maar eigenlijk zit het uitwerken van het vraagstuk vooral in de omzetting van de ene eenheid naar de andere via tussenstappen.
Verspreid over het vraagstuk gaat het over 'per dag' en 3 injecties, dus eigenlijk is er ook nog een verborgen eenheid: injecties / dag. Deze komt als een van de tussenstappen naar voren. Dit geldt ook voor de insuline: de bedoeling is 1 IE / kg per dag.
De vewreiste tussenstappen laten zich bewerken als breuken.
Optellen en aftrekken van breuken is alleen mogelijk als zij dezelfde noemer hebben. Vermenigvuldigen gaat door tellers met elkaar te vermenigvuldigen en noemers met elkaar.
Maar eerst kijk je of in de teller van de ene breuk hetzelfde getal staat als in de noemer van de andere breuk. Als dat zo is, kun je die tegen elkaar wegstrepen: 3/8 x 8/10 = 3/10. De 8 in de noemer en de 8 in de teller vallen dus tegen elkaar weg. Bovendien is delen door een breuk gelijk aan vermenigvuldigen met het omgekeerd.;
Voor je de som gaat uitwerken moet je jezelf nog afvragen: zijn alle eenheden bekend? Weet je bijv. wat een IE is? IE staat namelijk voor een Injectie Eenheid, dus de hoeveelheid die per injectie ingespoten wordt.
Analyse:
In feite moet je bij het lezen van het vraagstuk een stappenplan voor de berekening vaststellen, die begint bij de gegevens en eindigt bij de vraag. Maar om te weten wat je moet doen, moet je eigenlijk eerst van de vraag terug redeneren naar de beschikbare gegevens.
Als je dat een paar keer gedaan hebt, kun je op de toets de stappen dromen en direct van de gegevens naar de vraag gaan.
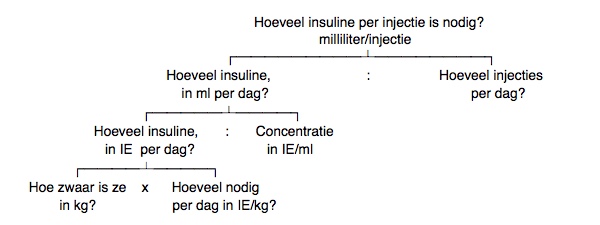
Uitwerking in 3 stappen:
1. Hoeveelheid insuline in IE per dag: 81 kg x 1 IE/kg per dag = 81 IE per dag
2. Hoeveelheid insuline in ml per dag: 81 IE per dag : 100 IE/ml = 0,81 ml per dag
3. Hoeveelheid insuline per injectie: 0,81 ml per dag : 3 injecties per dag = 0,27 ml/injectie.
Dus het antwoord is: 0,27 ml per injectie.
Rekenkundige uitwerking, waarbij de toevoeging 'per dag' vanzelfsprekend is:
81 kg x 1 IE per kg = 81 IE
81 IE : 100 IE per ml = 0,81 ml
0,81 ml : 3 injecties= 0,27 ml / injectie
Eenheden verhouden zich net als breuken:
1. kg x IE/kg = iE,
net zoals 8 x 3/8 = 3
(teller en noemer zijn gelijk en vallen tegen elkaar weg)
2. IE : IE/ml = IE x ml/IE = ml,
net zoals 8 : 8/3 = 8 x 3/8 = 3
(delen door een breuk is vermenigvuldigen met het omgekeerde)
3. ml : aantal injecties = ml/injectie,
net zoals 8 : 3 = 8/3
(een getal delen door een ander getal geeft een breuk) .
Verdere uitwerking
Een verdere analyse van het gebruik van verborgen paden en complexe eenheden is te vinden op de website: Verpleegkundig rekenen. Daar staan meer typen van vraagstukken over het verpleegkundig rekenen uitgewerkt.
Alle blogs over de zeven invalshoeken van vakdidactiek
In totaal zijn de volgende blogs verschenen, waarin de zeven invalshoeken voor vakdidactiek successievelijk terugkomen. Bij een aantal blogs zijn een of meer voorbeelden toegevoegd. Daarnaast is er een blog met achtergrond informatie over de zeven invalshoeken waarin onderdelen nader uitgewerkt of toegelicht staan om veelvuldige herhaling te voorkomen.
De zeven invalshoeken voor vakdidactiek (achtergrondinformatie):
- Becommentariëren en verbeteren van bestaande lesprogramma;
- Beschrijven van de mentale voorstelling die docenten hebben
van hun vak;
- Voorbeeld 2.a De namen van leerlingen leren;
- Expliciteren van het instructieproces tijdens het onderwijs;
- Voorbeeld 3.a De vele talen van de wiskunde;
- Voorbeeld 3.b Goed lezen bestaat uit drie onderdelen;
- Voorbeeld 3.c Het verborgen pad;
- Voorbeeld 3.d Het gebruik van eenheden;
- Voorbeeld 3.e Verpleegkundig rekenen bijvoorbeeld;
- Stimuleren van de motivering van leerlingen door de vorm
van het lesaanbod;
- Bevorderen van de zelfsturing van leerlingen door eigen
organisatie van het onderwijs;
- Analyseren van de problemen die leerlingen hebben met de stof;
- Voorbeeld 6.a Rekenen met procenten;
- Onderzoeken welke mentale modellen leerlingen ontwikkelen
en toepassen;
- Voorbeeld 7.a Onderzoek via hardop-denk-sessies;
- Voorbeeld 7.b Op zoek naar gokstrategieën.
- Voorbeeld 7.c Wanneer ken je een hoofdstuk?
Bronnen
- Norman, D.A., Gentner, D.R. & Stevens, A.L. (1976), Comments on
learning schemata and memory representation. In D. Klahr (ed.),
Cognition and Instruction, Hillsdale N.J. Lawrence Erlbaum Ass.
- Sophie. Column: Nieuwe interessante onderwerpen en lastige toetsen,
Factor D, 2022, nummer 1, blz 11.
- Van Dongen, H. en Van der Meche, E., Mentale Modellen, Factor D, 2022,
nummer 1, blz 13.
- Vernooij F., De toetsende tucht van de dimensie-analyse. Maandblad
voor Accountancy en Bedrijfseconomie 67e jaargang, 1993, nr 10.
- Vernooij F., De toetsende tucht van de dimensie-analyse. Maandblad
voor Accountancy en Bedrijfseconomie, 68e jaargang 1994, nr 9, blz. 506.
- Vernooij, F., Een mentaal model van vakdidactiek. Factor D, 2022,
nummer 2, blz.17.
- Vernooij, F., Bedrijfseconomische begrippen en hun eenheden.
Zie: bedrijfseconomische-begrippen.nl.
Persoonsgegevens
Fons Vernooij was Vakdidacticus bedrijfseconomie en algemene economie bij het ILO in Amsterdam en is nu met pensioen. Hij beheert de website vakdidactiek.nl als onderdeel van zijn website onderwijsportaal.nl. Vanwege zijn achtergrond zijn veel voorbeelden ontleend aan de economische vakken.
Als vakdidacticus voerde hij in 1993 een promotieonderzoek uit. Zie: Vernooij, F., (1993), Het leren oplossen van bedrijfseconomische problemen. Proefschrift, te vinden op vakdidactiek-bedrijfseconomie.nl.
Deze blogs zijn een uitvloeisel van zijn artikel “Een mentaal model van vakdidactiek”, dat is verschenen in het blad Factor D (didactiek), veertigste jaargang, nummer 2 uit 2022. Dit artikel is te downloaden via www.fons-vernooij.nl/documenten/een-mentaal-model-van-vakdidactiek.pdf.
|